Reinforcement Learning Background

Reinforcement Learning Background#

Reinforcement learning (RL) is one of the three main paradigms of machine learning, along with supervised and unsupervised learning. RL defines a mathematical formalism for learning-based decision-making from experience, developing from the idea that learning in nature is based on the interaction with the environment. An RL agent aims to find the optimal policy to take actions that maximize a cumulative reward function. The reward function determines the quality of the actions regarding the agent’s interaction with the environment. The agent is trained via goal-directed learning in an environment where it can explore and exploit actions and their reward.

Reinforcement learning differs from other machine learning paradigms through its automated and integrated approach to data acquisition. Unlike in traditional machine learning, where data is typically assumed to be independently and identically distributed (i.i.d.), RL data is collected from a sequential process, influenced by the agent’s actions. Furthermore, RL optimization is not driven by ground truth outputs but by evaluating the agent’s success or failure in completing tasks, as determined by the reward signal received from the environment.

The trade-off between exploration and exploitation is one of the key aspects introduced by RL. To accumulate the most reward, the agent must exploit the best actions it has learned so far, but also explore new actions that might lead to even higher rewards. The agent must balance between these two aspects to maximize the cumulative reward.

This chapter will introduce the fundamental concepts of reinforcement learning and the various classes of solution methods used to address the problem. The structure of this introduction follows the framework proposed by Sutton and Barto in Reinforcement Learning: An Introduction [2] . The final section will provide an overview of the algorithms utilized in this research and in related studies.

The Reinforcement Learning Problem#

In an RL system, the agent defines the learner and the decision-maker. The agent interacts with the environment, which is the external system, by taking actions (\(a \in A\)). The agent’s actions modify the environment state (\(s \in S\)) observed by the agent, and the environment provides feedback to the agent in the form of a reward signal (\(r \in R\)).

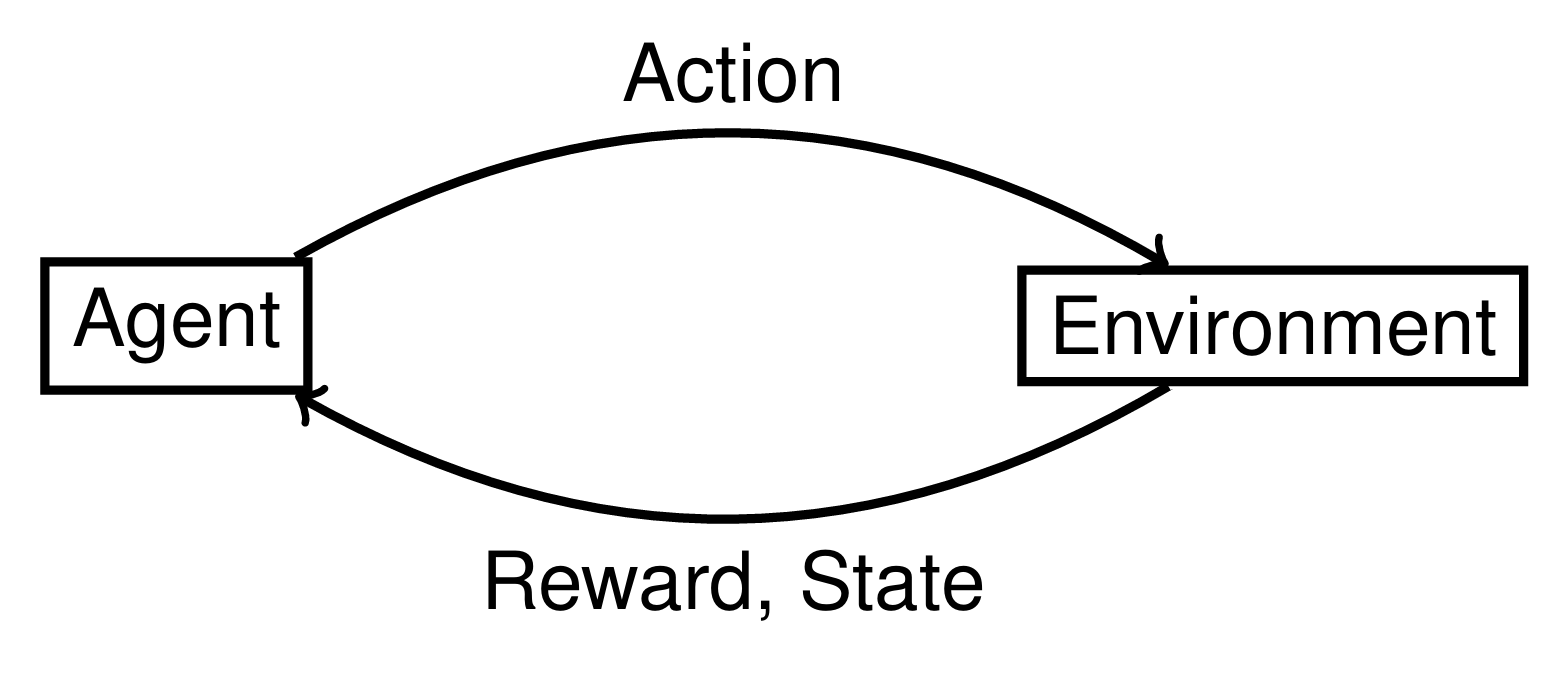
../_images/rl_loop.png

Fig. 13 Reinforcement Learning Loop: The agent selects an action that affects the environment. The environment responds with a new state and a reward signal to the agent.#

This interaction forms a loop that repeats over time, as shown in Figure Fig. 13. The agent observes the state \(s_t\) of the environment, selects an action \(a_t\) based on the policy \(\pi\), and receives a reward \(r_t\) from the environment. The action changes the environment, which transitions to the next state \(s_{t+1}\), and the loop repeats.

During the process, the agent learns from the interaction with the environment by updating its policy based on the rewards received. The goal of the agent is to learn the optimal policy \(\pi^*\) that maps states to actions, to maximize the cumulative reward over time.

The entire system relies on the state, serving as both the input and output of the agent’s interaction with the environment. Formally, a state is defined within the framework of a Markov Decision Process (MDP).

Markov Decision Process#

RL is usually modeled as a Markov Decision Process (MDP) [3]. An MDP describes a sequential fully observable decision process, where for each state \(s_t\) there is a possible set of actions \(a \in A\) and a transition model that defines the probability of transitioning to the next state \(s_{t+1}\) given the current state \(s_t\) and action \(a_t\):

\[P(s_{t+1}) = P(s_{t+1} \mid s_t, a_t)\]

which is called state transition probability.

In a Markov process, the state is expected to fulfill the Markov property, meaning that the future state depends only on the current state and action, and is independent of the sequence of states and actions that preceded it. This implies that the current state contains all the information of the past states. The Markov property is defined as:

\[P(s_{t+1} \mid s_t, a_t, s_{t-1}, a_{t-1}, \ldots) = P(s_{t+1} \mid s_t, a_t)\]

which signifies that the future state is conditionally independent from the past.

Partial Observability#

In many real-world scenarios, agents cannot fully observe the state of the environment and must rely on partial and noisy observations. This situation is modeled by a Partially Observable Markov Decision Process (POMDP) [4] . A POMDP extends the Markov Decision Process (MDP) framework by incorporating a set of observations and an observation function, which specifies the probability of observing a particular observation given the current state and action taken.

In a POMDP, the agent maintains a belief state, a probability distribution over all possible states, updated based on actions taken and observations received using Bayes’ theorem. The belief state \(b(s)\) represents the agent’s estimate of being in the state \(s\) given its history of actions and observations. The update of the belief state after taking action \(a\) and receiving observation \(o\) is given by:

\[b'(s') = \frac{O(o \mid s', a) \sum_{s \in S} P(s' \mid s, a) b(s)}{\sum_{s' \in S} O(o \mid s', a) \sum_{s \in S} P(s' \mid s, a) b(s)},\]

where \(b'\) is the updated belief state, \(O\) is the observation probability function, and \(P\) is the state transition probability function [4] . The goal of a POMDP is to find a policy \(\pi(b)\) that maps belief states onto actions to maximize the expected cumulative reward. Unlike MDPs, where decisions are made based on the true state, POMDPs require decisions based on the belief state to account for uncertainty in perception.

State#

In a reinforcement learning (RL) system, the state \(s \in S\) represents the complete information about the environment at each time step. In environments where all relevant information is observable, \(s\) directly reflects the system’s status and is used by the agent to make decisions.

However, in partially observable environments the agent does not have direct access to the complete state. Instead, it receives observations \(o\), which provide partial or noisy information about the true state. Despite this, the term state \(s\) is used throughout for consistency. The distinction between fully observable and partially observable environments is understood from the context. In fully observable settings, \(s\) represents the complete state, while in partially observable settings, \(s\) is inferred from the observations \(o\).

Episode and Horizon#

In a RL system, the interaction between the agent and the environment is usually divided into episodes. An episode is a sequence of states, actions, and rewards that starts at the initial state and ends when a terminal state \(s_T\) is reached, at the time step \(T\). The environment is then reset to the initial state to start a new episode independent of the previous. The sequence of states, actions, and rewards in an episode is called trajectory.

Tasks with a determined terminal state, like reaching a determined position or winning a game, are called episodic tasks and are said to have a finite horizon, ending at a specific time step \(T=t_{end}\). Tasks that do not have a terminal state, like balancing a pole or driving a car, are called continuous tasks and are said to have an infinite horizon, hence \(T=\infty\).

Core Elements of a Reinforcement Learning System#

The main elements of an RL system beyond the agent and the environment are a policy \(\pi\), a reward signal \(r\), a value function \(V(s)\), and a model of the environment \(P(s_{t+1}, r_t | s_t, a_t)\) [2] .

Policy#

The policy \(\pi(s)\) is the agent’s strategy, or the way it selects actions in each state, to maximize the total reward. It maps the state perceived from the last observations to the set of actions the agent can take. It can be deterministic (1) or stochastic (2), and can be represented as a function that maps states to actions. The policy can be a simple function, such as a lookup table, or a complex function, such as a deep neural network.

(1)#\[\begin{split}\begin{gathered} \pi: S \rightarrow A \\ \pi(s) = a \\ \end{gathered}\end{split}\]
(2)#\[\pi(a \mid s) = P[A_t = a \mid S_t = s]\]

Reward Signal and Return#

The reward signal is the feedback the agent receives from the environment after each action. It is a scalar value that indicates how well the agent is doing at a given time step. The goal of the agent is to maximize the cumulative reward over time.

Formalizing the idea of a goal with a reward signal is a key aspect that distinguishes RL from other machine learning paradigms, and allows for flexibility and wide applicability. The definition of the reward signal is a crucial aspect of the RL problem, as it determines the agent’s behavior and the quality of the learned policy.

The cumulative reward is defined by the concept of return, denoted by \(G_t\), which is a function of the reward sequence. In the simplest case, the return is the sum of the rewards received from a given time step onwards:

\[G_t = R_{t+1} + R_{t+2} + \ldots + R_T\]

Returns can be discounted, to give more importance to immediate rewards, or to avoid infinite returns in continuous tasks. The discounted return is defined as:

\[G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \ldots = \sum_{k=0}^{T} \gamma^k R_{t+k+1}\]

Where \(\gamma\) is the discount factor, \(0 \leq \gamma \leq 1\). The discount factor determines the importance of future rewards and its value is a design choice that depends on the task. A \(\gamma\) close to 0 gives more importance to immediate rewards, while a \(\gamma\) close to 1 gives more importance to future rewards.

Returns can be computed step-by-step, or in a recursive way, as the sum of the immediate reward and the discounted return from the next time step:

\[\begin{split}\begin{aligned} G_t & = R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\gamma^3 R_{t+4}+\cdots \\ & =R_{t+1}+\gamma\left(R_{t+2}+\gamma R_{t+3}+\gamma^2 R_{t+4}+\cdots\right) \\ & =R_{t+1}+\gamma G_{t+1} \end{aligned}\end{split}\]

Value Function#

The value function is a prediction of the expected long-run reward that the agent can expect to receive from a given state onwards. Compared to the reward, which determines the immediate advantage of being in a certain state, the value function estimates how good it is to be in a state in a long-term perspective, taking into account the states that are likely to follow and their expected reward. Another main difference is that rewards are received from the environment, so they are a primary source of feedback for the agent, while the value function is learned by the agent, and must be estimated iteratively. The value function can be represented as a function that maps states to values, and can be learned using different methods, such as dynamic programming, Monte Carlo methods, or temporal difference learning.

The value function can be defined in two ways: the state-value function \(V_{\pi}(s)\), which estimates the expected return starting from a state \(s\) and following the policy \(\pi\), which is defined as

\[V_{\pi}(s) = E[G_t \mid S_t = s], \quad \forall \: s \in S,\]

and the action-value function \(Q_{\pi}(s, a)\), or Q-function as it is often called, which estimates the expected return after taking an action \(a\) in a state \(s\) and following the policy \(\pi\) thereafter, defined as

\[Q_{\pi}(s, a) = E[G_t \mid S_t = s, A_t = a], \quad \forall \: s \in S, a \in A.\]

Model of the Environment#

A model of the environment is an optional component of a RL system that learns to infer the environment’s dynamics. Models are used for planning a course of action based on the current state of knowledge. The use of a model characterizes model-based RL, as opposed to model-free RL, where the agent learns directly by trial-and-error interaction with the environment.

Bellman Equation and Optimal Policy#

The Bellman equation is a key concept in RL that defines the relationship between the value of a state and the value of its successor states in a recursive way, that can be expressed in terms of the state-value function,

(3)#\[ \begin{align}\begin{aligned}\begin{split}\begin{aligned} V_\pi(s) & =E_\pi\left[G_t \mid S_t=s\right] \\ & =E_\pi\left[R_{t+1}+\gamma G_{t+1} \mid S_t=s\right] \\ & =\sum_a \pi(a \mid s) \sum_{s'} \sum_r p\left(s', r \mid s, a\right)\left[r+\gamma E_\pi\left[G_{t+1} \mid S_{t+1}=s'\right]\right] \\ & =\sum_a \pi(a \mid s) \sum_{s', r} p\left(s', r \mid s, a\right)\left[r+\gamma V_\pi\left(s'\right)\right], \quad \forall \: s \in S, \end{aligned}\end{split}\\.\end{aligned}\end{align} \]

or the action-value function,

(4)#\[ \begin{align}\begin{aligned}\begin{split}\begin{aligned} Q_\pi(s, a) & =E_\pi\left[G_t \mid S_t=s, A_t=a\right] \\ & =E_\pi\left[R_{t+1}+\gamma G_{t+1} \mid S_t=s, A_t=a\right] \\ & =\sum_{s', r} p\left(s', r \mid s, a\right)\left[r+\gamma E_\pi\left[G_{t+1} \mid S_{t+1}=s'\right]\right] \\ & =\sum_{s', r} p\left(s', r \mid s, a\right)\left[r+\gamma V_\pi\left(s'\right)\right] \\ & =\sum_{s', r} p\left(s', r \mid s, a\right)\left[r+\sum_{a'} \pi\left(a' \mid s'\right) Q_\pi\left(s', a'\right)\right], \quad \forall \: s \in S, a \in A. \end{aligned}\end{split}\\.\end{aligned}\end{align} \]

Solving the RL problem means finding the optimal policy \(\pi^*\) that maximizes the return at each state. The optimal policy is thus the one that follows the optimal value function \(V^*\), which is defined as the maximum expected return that can be achieved by following the policy \(\pi\):

\[V^*(s) = \max_{\pi} V_\pi(s), \quad \forall \: s \in S\]

The optimal action-value function \(Q^*(s, a)\) is similarly defined as

\[Q^*(s, a) = \max_{\pi} Q_\pi(s, a), \quad \forall \: s \in S, a \in A,\]

and can be expressed in terms of \(V^*(s)\) as

\[Q^*(s, a) = E\left[R_{t+1} + \gamma V^*(S_{t+1}) \mid S_t = s, A_t = a\right].\]

The Bellman equation can be used to define the optimal state-value function \(V^*(s)\), which can be expressed independently from any \(\pi\). The Bellman’s optimality equation for \(V^*\) represents the maximum expected return that can be achieved from each state by choosing the best possible action. Therefore, \(V^*(s)\) is equal to the optimal action-value function \(Q^*(s, a)\) for the best action \(a\):

\[\begin{split}\begin{aligned} V^*(s) & = \max_{a \in A(s)} Q_{\pi^*}(s, a) \\ & = \max_{a} E_{\pi^*}[G_t | S_t = s, A_t = a] \\ & = \max_{a} E_{\pi^*}[R_{t+1} + \gamma G_{t+1} | S_t = s, A_t = a] \\ & = \max_{a} E_{\pi^*}[R_{t+1} + \gamma V^*(S_{t+1}) | S_t = s, A_t = a] \\ & = \max_{a} \sum_{s', r} p(s', r | s, a) \left[r + \gamma V^*(s')\right] \end{aligned}\end{split}\]

The Bellman optimality equation for the optimal action-value function \(Q^*(s, a)\) is defined as

\[\begin{split}\begin{aligned} Q^*(s, a) & = E[R_{t+1} + \gamma \max_{a'} Q^*(S_{t+1}, a') | S_t = s, A_t = a] \\ & = \sum_{s', r} p(s', r | s, a) \left[r + \gamma \max_{a'} Q^*(s', a')\right] \end{aligned}\end{split}\]

The optimal policy \(\pi^*\) can be derived from the optimal action-value function \(Q^*(s, a)\) by selecting the action that maximizes the expected return from each state:

\[\pi^*(s) = \arg\max_a Q^*(s, a),\]

without the need to know anything more about the successor states. As a result, many RL algorithms prioritize learning the Q-value function, as it suffices to derive the optimal policy.

On-Policy vs Off-Policy Reinforcement Learning#

Reinforcement learning algorithms can be broadly categorized into two types based on how they use the data collected from the environment: on-policy and off-policy. The distinction between on-policy and off-policy methods lies in how they update the policy and learn the value function.

On-policy algorithms learn the value of the policy that is simultaneously used to select actions. This means that they improve the policy that is used to make decisions as they interact with the environment. The policy is updated based on the value function, and the value function is updated based on the policy. This can lead to a more stable learning process, but it can also limit exploration and the ability to learn an optimal policy.

Off-policy algorithms learn the value of an optimal policy independently of the policy used for exploration. One is called target policy, and the other is called behavior policy. This allows off-policy methods to learn from data generated by any policy, including random or expert policies.

The expected value function of the target policy is estimated using the data collected by the behavior policy utilizing importance sampling. Using this technique, it is possible to weigh the returns according to the relative probability of the actions taken by the two policies:

\[\begin{split}\begin{gathered} Q^{\pi}(s, a) = \frac{\sum_{t} \rho_t G_t}{\sum_{t} \rho_t}, \\ \text{where} \; \rho_t = \prod_{k=t}^{T-1} \frac{\pi(A_k \mid S_k)}{b(A_k \mid S_k)}, \end{gathered}\end{split}\]

where \(\rho_t\) is the importance sampling ratio, \(\pi\) is the target policy, and \(b\) is the behavior policy.

Solution Methods for Reinforcement Learning#

Reinforcement learning problems can be solved using various methods, depending on the availability of the model, the complexity of the environment, and the observations collected from the interaction with the environment.

Dynamic Programming#

If the model of the environment is available, which means the transition probabilities \(p(s', r | s, a)\) are known, the optimal policy can be computed using Dynamic Programming (DP) methods. DP algorithms solve the Bellman equation iteratively, updating the value function until it converges to optimality.

Classical dynamic programming (DP) algorithms are theoretically significant but have limited practical use in reinforcement learning due to their reliance on a perfect model and high computational cost. However, they provide a crucial foundation for understanding modern RL methods, which aim to achieve similar results with less computation and without assuming a perfect model of the environment [2] .

Policy Evaluation#

Policy evaluation is the process of estimating the value function \(V_\pi(s)\) or \(Q_\pi(s, a)\) for a given policy \(\pi\) by solving the Bellman equation in (3) or (4).

Policy Improvement#

Policy improvement is the process of updating the policy based on the value function to select the best action in each state. The policy is updated by selecting the action that maximizes the expected return:

\[\pi'(s) = \arg\max_a Q_\pi(s, a), \quad \forall \: s \in S.\]

Generalized Policy Iteration#

Policy iteration is an iterative algorithm that alternates between policy evaluation and policy improvement until the policy converges to the optimal policy. In each iteration, the policy is evaluated using the current value function and then improved by selecting the best action in each state. The process continues until the policy no longer changes, at which point the optimal policy has been found.

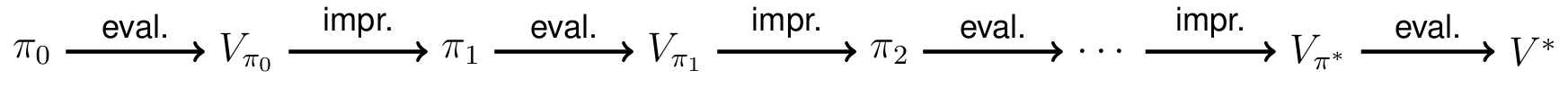
../_images/policy_iteration.png

Monte Carlo Methods#

Monte Carlo (MC) methods are a class of model-free reinforcement learning algorithms that estimate value functions based on averaging the returns observed from multiple episodes. Unlike Dynamic Programming, Monte Carlo methods do not require a model of the environment. Instead, they learn directly from experience by collecting samples of the transitions and rewards from the trajectory.

Policy Evaluation#

In Monte Carlo policy evaluation, the value function \(V_\pi(s)\) or \(Q_\pi(s, a)\) for a given policy \(\pi\) is estimated by averaging the returns following each state or state-action pair. The value is updated based on the observed returns:

\[V_\pi(s) \approx \frac{1}{N} \sum_{i=1}^{N} G_t^{(i)},\]

where \(G_t^{(i)}\) is the return following state \(s\) in the \(i\)-th episode, and \(N\) is the number of episodes in which \(s\) is visited.

Exploring Starts and \(\epsilon\)-Greedy Policies#

Monte Carlo methods often rely on exploring starts or \(\epsilon\)-greedy policies to ensure sufficient exploration of the state space. Exploring starts involve starting episodes from every state-action pair, while \(\epsilon\)-greedy policies involve selecting a random action with probability \(\epsilon\) and the best action with probability \(1 - \epsilon\).

Temporal Difference Learning#

Temporal Difference (TD) learning methods are a class of model-free reinforcement learning algorithms that combine ideas from MC methods and DP. TD methods learn directly from raw experience without a model of the environment, but, unlike MC methods, they update value estimates without waiting for the end of the episode. The following are some examples of popular TD algorithms.

TD(0)#

TD(0), or one-step TD learning, updates the value function \(V_\pi(s)\) based on the observed reward and the estimated value of the next state:

\[V(s_t) \leftarrow V(s_t) + \alpha \left[ R_{t+1} + \gamma V(s_{t+1}) - V(s_t) \right],\]

where \(\alpha\) is the learning rate and \(\gamma\) is the discount factor. This update rule is applied at each time step, making TD(0) an online learning algorithm.

SARSA: On-Policy TD control#

An example of an on-policy TD algorithm is the SARSA Algorithm[5] . The name SARSA comes from the sequence of states and actions used to update the Q-values: it starts from a state \(s\), takes action \(a\), receives a reward \(r\), moves to the next state \(s'\), and then takes action \(a'\).

\[Q(s, a) \leftarrow Q(s, a) + \alpha [r + \gamma Q(s', a') - Q(s, a)]\]

The agent uses its current policy to interact with the environment. For each step, it updates the Q-value. The policy is updated to favor actions with higher Q-values. The problem with on-policy methods is that the agent’s exploration strategy is directly tied to the policy, which can limit the exploration of new actions.

Q-Learning: Off-Policy TD control#

A classic example of an off-policy TD algorithm is Q-Learning [6] .In Q-Learning, the agent updates its Q-values based on the maximum future rewards achievable, regardless of the action which is actually taken in the next step. This means that the agent can learn the optimal policy even while following a different (exploratory) policy.

\[Q(s, a) \leftarrow Q(s, a) + \alpha [r + \gamma \max_{a'} Q(s', a') - Q(s, a)]\]

Off-policy methods like Q-Learning are more data-efficient because they can learn from past experiences stored in a replay buffer, while on-policy methods require fresh data from the current policy. However, they are more prone to instability due to the mismatch between the behavior and target policies.

TD(\(\lambda\))#

TD(\(\lambda\)) is a temporal difference learning method that generalizes TD(0) by incorporating ideas from both TD learning and Monte Carlo methods. The core idea of TD(\(\lambda\)) is to update the value estimate for a state \(s_t\) using a weighted average of the TD errors over multiple n-step updates, each weighted proportionally to \(\lambda^n(n-1)\), and normalized by \((1-\lambda)\) to ensure the weights sum up to 1:

\[V_\lambda(s_t) = (1-\lambda) \sum_{n=1}^{\infty} \lambda^{n-1} V_n(s_t),\]

where \(V_n(s_t)\) is the n-step value estimate for state \(s_t\). TD(\(\lambda\)) balances bias and variance in the value estimates, providing a flexible framework that encompasses both TD(0) and Monte Carlo methods.

Function Approximation#

In many practical reinforcement learning problems, the state or state-action space is too large to be represented explicitly. In such cases, function approximation methods are used to generalize the value function or policy over the state space using a parameterized function. The generalization from observed states to unobserved states enables RL algorithms to scale to larger problems. Compared to supervised learning, the data is usually collected from experience on the run, and the target values are not fixed, but are updated iteratively.

The mean squared value error is a common loss function used to train the function approximator, defined as

\[\overline{VE}(\mathbf{w}) = \sum_{s \in S} \mu(s) {[V_{\pi}(s) - \hat{V}(s, \mathbf{w})]}^2,\]

where \(\hat{v}(s, \mathbf{w})\) is the approximated value function, \(\mathbf{w}\) are the weights of the function approximator, and \(\mu(s)\) is the distribution of states. The distribution \(\mu(s)\) expresses how often a state is visited and is used to weight the error based on the importance of the state. The objective is to minimize the mean squared value error by adjusting the weights \(\mathbf{w}\).

Stochastic Gradient Descent#

One solution to minimize the mean squared value error is to use stochastic gradient descent (SGD) to update the weights \(\mathbf{w}\) of the function approximator. The weights are adjusted in the direction of the negative gradient of the loss function \(\overline{VE}(\mathbf{w})\) with respect to the weights:

\[\begin{split}\begin{aligned} \mathbf{w_{t+1}} & = \mathbf{w_t} - \frac{1}{2} \alpha \nabla_{\mathbf{w}} \overline{VE}(\mathbf{w}) \\ & = \mathbf{w_t} + \alpha \left[ V_{\pi}(s) - \hat{V}(s, \mathbf{w}) \right] \nabla_{\mathbf{w}} \hat{V}(s, \mathbf{w}), \end{aligned}\end{split}\]

where \(\alpha\) is the learning rate. The gradient is estimated using samples from the state distribution \(\mu(s)\).

Linear Function Approximation#

Linear function approximation represents the value function as a linear combination of features:

\[\hat{V}(s) \approx \mathbf{w}^T \mathbf{\phi}(s), \quad \hat{Q}(s, a) \approx \mathbf{w}^T \mathbf{\phi}(s, a),\]

where \(\mathbf{w}\) is a weight vector and \(\mathbf{\phi}(s)\) or \(\mathbf{\phi}(s, a)\) is a feature vector. The weights are adjusted using gradient descent based on the TD error or the observed return.

Non-Linear Function Approximation#

Non-linear function approximation, such as neural networks, can represent more complex value functions or policies. Deep Q-Networks (DQN) [7][8] is a prominent example, where a neural network is used to approximate the Q-function. The network is trained using a variant of Q-learning:

\[\theta \leftarrow \theta + \alpha \left( R_{t+1} + \gamma \max_{a'} \hat{Q}(s_{t+1}, a'; \theta^-) - \hat{Q}(s_t, a_t; \theta) \right) \nabla_\theta \hat{Q}(s_t, a_t; \theta),\]

where \(\theta\) are the network parameters, and \(\theta^-\) are the parameters of a target network that is periodically updated to stabilize training.

Experience Replay and Target Networks#

Experience replay and target networks are techniques used in conjunction with function approximation to improve stability and performance. Experience replay stores transitions in a replay buffer and samples mini-batches to train the network. This reduces the correlation between samples and improves data efficiency.

Target networks are used to stabilize training by fixing the target Q-values for a fixed number of steps. The target network is updated periodically with the parameters of the online network, reducing the variance in the Q-value estimates.

Policy Gradient Methods#

Policy gradient methods directly parameterize and optimize the policy, rather than the value function. They learn the policy by updating the policy parameters in the direction of the expected return [9] :

(5)#\[ \begin{align}\begin{aligned}\begin{split}\begin{gathered} \pi(a \mid s, \theta) = P[a_t \mid s_t, \theta_t], \\ \theta \leftarrow \theta + \alpha \nabla_\theta \hat{J}(\theta), \\ \text{where} \; \hat{J}(\theta) = E_\pi [G_t | \theta]. \end{gathered}\end{split}\\.\end{aligned}\end{align} \]

Policy gradient methods are often employed in continuous action spaces and have proven effective in high-dimensional and complex environments. These methods are advantageous due to their ability to learn stochastic policies and their compatibility with continuous action spaces. Additionally, they can incorporate prior knowledge or constraints on the policy.

To compute the update, the policy must be differentiable with respect to the parameters \(\theta\) so that the gradient can be calculated. The gradient of the expected return is proportional to the gradient of the policy times the Q-value of each possible action in each state, multiplied by the state distribution factor \(\mu\):

(6)#\[\begin{split}\begin{aligned} \nabla_\theta \hat{J}(\theta) & \propto \sum_{s \in S} \mu(s) \sum_{a \in A} Q_{\pi_{\theta}}(s, a) \nabla_\theta \pi(a \mid s, \theta) \\ & = E_{\pi_{\theta}} \left[ Q_{\pi_{\theta}}(s, a) \nabla_\theta \ln \pi(a \mid s, \theta) \right]. \end{aligned}\end{split}\]

REINFORCE Algorithm#

The REINFORCE algorithm [10] is a Monte Carlo policy gradient method that updates policy parameters \(\theta\) in the direction of the expected return:

(7)#\[\theta \leftarrow \theta + \alpha \sum_{t=0}^{T} \gamma^t G_t \nabla_\theta \log \pi_\theta(a_t | s_t),\]

Although REINFORCE is straightforward to implement, it suffers from high variance due to the Monte Carlo estimation of the return. To mitigate this, variance reduction techniques such as baseline subtraction or advantage estimation are commonly employed to stabilize training. Baseline subtraction involves subtracting a baseline value, typically the value function \(V(s)\), from the return. This encourages the agent to take actions that outperform the average, thereby reducing variance.

Actor-Critic Methods (A2C)#

The main advantage of policy gradient methods is their direct approach to optimizing the desired objective - the policy - which generally makes them stable and reliable. In contrast, Q-learning methods aim to enhance agent performance indirectly, by training to fulfill a self-consistency equation between behavior and target policy, which introduces numerous potential failure modes and makes them less stable [11] . However, when Q-learning methods are successful, they are significantly more sample-efficient as they can reuse data more effectively than policy optimization techniques.

Actor-Critic methods combine the advantages of policy gradient and value-based methods. They consist of two components: an actor, which updates the policy, and a critic, which estimates the value function. The policy update relies on the advantage function

\[A(s_t, a_t) = Q(s_t, a_t) - V(s_t),\]

which incorporates the concept of baseline subtraction to reduce variance. By subtracting the value function from the Q-value, the advantage function ensures that the policy is updated positively for actions that yield a higher value than the average state value and negatively for actions that perform worse. The actor’s weight update rule is:

\[\theta \leftarrow \theta + \alpha A(s_t, a_t) \nabla_\theta \log \pi_\theta(a_t | s_t),\]

The critic, on the other hand, can be trained to estimate the value function using TD learning or other value-based methods.

Deep Reinforcement Learning Algorithms#

Deep Reinforcement Learning (DRL) is a subfield of reinforcement learning that combines deep learning with RL to learn complex policies from high-dimensional input data. It has soon become the dominant approach in solving challenging RL problems because of its ability to handle high-dimensional state spaces and continuous action spaces [11][12] .

A great overview of the topic with references to the foundational papers, as well as a collection of implementations, recommendations, and tutorials on the topic can be found in the ‘Spinning Up’ documentation offered by OpenAI [1] [13] . This section provides an overview of four prominent RL algorithms which have been used in this work or the related research: Deep Q-Learning, Asynchronous Advantage Actor-Critic (A3C), Proximal Policy Optimization (PPO), and Soft Actor-Critic (SAC).

Deep Q-Learning#

Deep Q-Learning (DQN) was first proposed by Mnih et al. [7] to combine deep learning with reinforcement learning, and has been widely used in many applications. It introduced the concepts of experience replay and target networks to stabilize training [8] .

Deep Q-Learning extends Q-Learning to handle environments with high-dimensional state spaces by approximating the Q-function using a deep neural network, known as a Deep Q-Network (DQN). In the foundational paper, the authors trained an agent to play Atari games directly from raw pixel inputs, demonstrating the power of DRL in solving complex tasks.

The observation space of the agent consists of the frames from the games screen, preprocessed to grayscale and resized to fixed dimension. The last four frames are stacked to capture the motion of the game. The DQN consists of two convolutional layers followed by two fully connected layers, and the output is a vector of the action space dimension. The output corresponds to the Q-value of each action available in the current state, so it can be used to determine the best action. However, this limits the method to discrete action spaces, which means the action space consists of a finite number of discrete actions.

The method introduces the use of experience replay, storing the past transitions \((s, a, r, s')\) in a replay buffer and retrieving them on randomly sampled mini-batches to train the network. This randomization of the data helps to reduce the correlation between samples and smooth changes in the data distribution. Moreover, the target network is separated from the behavioral network and updated periodically. The behavioral policy network uses the fixed target values to compute the loss, thereby reducing the variance and the fluctuation of the Q-values and stabilizing training.

Asynchronous Advantage Actor-Critic (A3C)#

The use of an experience replay buffer and target networks in DQN limits the method to off-policy learning, because it updates the target policy with the data stored in the replay buffer, which has been generated by an older policy. The Asynchronous Advantage Actor-Critic (A3C) [14] algorithm proposes a classical policy gradient method with a special focus on parallelization which allows on-policy learning.

A3C asynchronously trains multiple agents in parallel to interact on different instances of the same environment. It uses an actor-critic architecture with multiple actors and a shared global critic. Each agent interacts with its own copy of the environment and updates the global critic network with its experiences.

The actor updates the policy in the direction of the advantage function, which is the difference between the Q-value and the value function. The critic estimates the value function using TD learning. This parallelization increases data efficiency and exploration, leading to faster convergence and better performance.

Proximal Policy Optimization#

Proximal Policy Optimization (PPO) [15] is an on-policy algorithm designed to improve the stability of policy gradient methods. It introduces a clipped objective function that restricts the extent of change allowed in each update step, ensuring that the new policy remains close to the previous one. This mechanism helps prevent drastic updates that could destabilize the learning process.

In policy gradient methods, the gradient estimator is used to optimize the expected return for the policy parameters \(\theta\), as shown in (6). Applying an advantage function \(A\) as a baseline, the gradient estimator takes the form

\[\nabla_\theta \hat{J}(\theta) = E_{\pi_{\theta}} \left[ A(s, a) \nabla_\theta \log \pi(a \mid s, \theta) \right].\]

The estimator is obtained by differentiating the objective function \(\hat{J}\) from (5), which can be expressed as:

\[\hat{J}(\theta) = E_{\pi_{\theta}} \left[ A(s, a) \log \pi(a \mid s, \theta)\right].\]

PPO uses a clipped objective function to prevent the policy from changing too much at each update. The clipped objective function is defined as:

\[\hat{J}^{\text{PPO}}(\theta) = E_t \left[ \min \left( r_t(\theta) \hat{A}_t, \text{clip} \left( r_t(\theta), 1 - \epsilon, 1 + \epsilon \right) \hat{A}_t \right) \right],\]

where \(r_t(\theta) = \frac{\pi_{\theta}(a_t \mid s_t)}{\pi_{\theta_{\text{old}}}(a_t \mid s_t)}\) is the probability ratio between the new and old policies, and \(\epsilon\) is a hyperparameter that controls the clipping, reducing the incentive for moving \(r_t\) out of the interval \([1 - \epsilon, 1 + \epsilon]\).

The clipped objective function in PPO ensures that the policy does not change excessively with each update, thereby preventing destabilization during learning. This means that for a favorable action, the policy update is constrained to a ratio no greater than \(1 + \epsilon\), and for an unfavorable one the update is constrained to a ratio no less than \(1 - \epsilon\).

Soft Actor-Critic Algorithm#

Soft Actor-Critic (SAC) [16][17] is an off-policy actor-critic DRL algorithm that incorporates the principle of policy maximum entropy in the objective function to encourage the agent’s exploration. This approach addresses the poor sample efficiency of on-policy algorithms, the stability issues associated with off-policy algorithms, and the sensitivity to hyperparameters inherent in both types of algorithms.

The RL objective from (5) is extended to include the maximum entropy term:

\[\hat{J}(\theta) = E_{\pi_{\theta}} \left[ \sum_{t=0}^{T} \gamma^t (r(s_t, a_t) + \alpha H(\pi_{\theta}( \cdot \mid s_t))) \right],\]

where \(H(\pi_{\theta}( \cdot \mid s_t))\) denotes the entropy of the policy, and \(\alpha\) is a temperature parameter that balances the entropy term with the reward. The introduction of entropy has several advantages, such as improved exploration, the ability to capture diverse near-optimal behaviors, and enhanced robustness and stability across different training runs.

As an actor-critic method, SAC utilizes distinct structures for updating the policy (actor) and estimating the value function (critic), and it leverages a replay buffer for experience replay. SAC employs three primary networks: a state-value function \(V_\psi(s)\), a Q-function \(Q_\theta(s, a)\), and a policy \(\pi_\phi(a \mid s)\), that are parameterized respectively by \(\psi\), \(\theta\), and \(\phi\). While, theoretically, a single value function could suffice, the separation into state-value and action-value functions in SAC is used to improve training stability and performance.

Additionally, SAC uses two Q-functions, \(Q_{\theta_1}(s, a)\) and \(Q_{\theta_2}(s, a)\), to mitigate positive bias in the policy update, a common issue in Q-learning methods. In particular, two \(Q_{\theta_i}\) are trained independently, and the minimum of the two Q-functions is used to compute the target value function and to update the policy.

The soft policy iteration consists of a first update of the state- and action-value functions’ parameters \(\psi\) and \(\theta\). The value network objective is to minimize the squared difference between the prediction of the value network and the expectation of the Q-function with the entropy term, which is measured by the negative log of the policy function:

\[J_V(\psi) = E_{s \sim \mathcal{D}} \left[ \frac{1}{2} {\left(V_\psi(s) - E_{a \sim \pi_\phi}[Q_{\theta}(s, a) - \alpha \log \pi_\phi(a \mid s)] \right)}^2 \right],\]

where \(\mathcal{D}\) denotes the replay buffer, the actions are sampled by the current policy and the the current Q-value function is used. This means rewarding actions with a high Q-value and high entropy.

The Q-function parameters are updated by minimizing the prediction of the Q-function and the immediate reward plus the discounted expected value of the next state:

\[J_Q(\theta) = E_{(s, a) \sim \mathcal{D}} \left[ \frac{1}{2} {\left(Q_{\theta}(s, a) - (r(s, a) + \gamma E_{s'}\left[V_{\overline{\psi}}(s')\right]) \right)}^2 \right],\]

where \(V_{\overline{\psi}}\) denotes the target value network. This is an expression of the advantage function that penalizes actions that are worse than the average value of the state.

Then, the policy parameters are updated by minimizing the Kullback-Leibler divergence between the policy and the exponential of the Q-function normalized by a partition function \(Z_\theta(s)\):

\[J_\pi(\phi) = E_{s \sim \mathcal{D}} E_{a \sim \pi_\phi} \left[ D_{KL}\left(\pi_\phi(\cdot \mid s) \parallel \frac{\exp(Q_{\theta}(s, \cdot))}{Z_\theta(s)}\right) \right],\]

meaning that it projects the policy towards the exponential of the normalized Q-function. Finally, the parameters of the target value network are updated by the soft policy iteration:

\[\overline{\psi} \leftarrow \tau \psi + (1 - \tau) \overline{\psi},\]

where \(\tau\) is a hyperparameter that controls the softness of the update.

Bibliography#

Contents